Codul proiectului: POCU/73/6/6/108182
Titlul proiectului: „ProForm - PROfesionalizarea cadrelor didactice prin FORMare continuă”
Beneficiar / Partener 1/ Partener 2: Asociaţia Societatea Naţională Spiru Haret pentru Educaţie, Ştiinţă şi Cultură
Numele și prenumele expertului: Albeanu Grigore
Poziția în cadrul proiectului: Expert programe formare profesională
Nr. și tipul contractului 229/01.05.2018/ CIM
Categorie expert: Expert termen lung
Inteligență computațională – calcul nuanțat
Expresia „inteligență computațională” se utilizează pentru a cuprinde anumite mecanisme computaționale din domeniul inteligenței artificiale: calcul nuanțat (sisteme fuzzy), calcul evolutiv (algoritmi genetici, programare genetică), calcul neuronal (folosind rețele neuronale artificiale) etc.
În cele ce urmează descriem un model care extinde raționamentul binar aplicat mulțimilor și logicii clasice. Se obțin expresiile care se referă la mulțimi fuzzy, respectiv logică fuzzy.
Funcția de apartenență utilizată în teoria clasică a mulțimilor se extinde de la codomeniul {0, 1} la intervalul [0, 1] care conține grade de apartenență. Mulțimea valorilor de adevăr {0 – fals, 1 – adevărat} se extinde la intervalul [0, 1] care conține grade de validitate a unei afirmații. Aceste extinderi au fost propuse de L. Zadeh [1]. Metode computaționale nuanțate pentru a rezolva diverse probleme concrete se află în [2].
Prezentăm, mai departe, câteva elemente de calcul nuanțat ce pot fi folosite la cercurile de elevi sau centrele de excelență.
O mulţime fuzzy A poate fi definită ca o mulţime de perechi (x, fA(x)), în care x in U, iar fA(x) este funcţia de apartenenţă, fA : U -> [0, 1]. De exemplu [3], Mulţimea fuzzy a numerelor naturale "nu prea mari" poate fi definită ca mulţimea A a perechilor {(1,1), (2,1), (3,1), (4,0.9), (5,0.8), (6,0.7), (7,0.6), (8,0.5), (9,0.3), (10,0.1), (11,0),(12,0),...}.Mulţimea universală în acest caz este mulţimea numerelor naturale, iar funcţia de apartenenţă este definită, evident, subiectiv
Utilizând funcţia de apartenenţă, operaţiile de determinare a complementarei unei mulţimi fuzzy A, a reuniunii şi a intersecţiei a două mulţimi fuzzy A şi Bsunt definite astfel:
Complementara unei mulţimi fuzzy A se numeşte mulţimea fuzzy Ā cu funcţia de apartenenţăfĀ(x)= 1-fA(x);
Reuniunea a două mulţimi fuzzy A şi B numim mulţimea fuzzy AÈB cu funcţia de apartenenţă fAUB(x) = max[fA(x), fB(x)];
Intersecţia a două mulţimi fuzzy A şi B numim mulţimea fuzzy AÇB cu funcţia de apartenenţa fAÇB(x) =min[fA(x), fB(x)];
Există şi alte definiţii ale ultimelor două operaţii.
Funcțiile de apartenență pot fi de tip triunghiular, trapezoidal, gaussian etc. Acestea, în general sunt stabilite de experți care cunosc domeniul pentru care se trece la raționamentul nuanțat in vederea unui proces decizional în condiții de imprecizie [5].
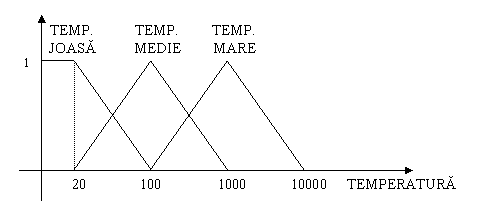
Zadeh a motivat următoarele caracteristici obligatorii ale logicii fuzzy [3]:
- în logica fuzzy raţionamentele exacte suntconsiderate caz particular al raţionamentelor aproximative;
- în logica fuzzy totul depinde de gradul de apartenenţă;
- orice sistem logic poate fi fuzzyficat;
- în logica fuzzy cunoştinţele sunt interpretate ca un set de restricţii flexibile (vagi) peste o mulţime de variabile;
- procesul de elaborare a unei concluzii logice este considerat un proces de extindere a restricţiilor flexibile.
Calcularea valorii de adevăr a unei reguli fuzzy se produce conform unor mecanisme, legate de domeniul de cercetare, mecanisme specifice domeniului, cunoştinţele unor experţi, intuiţie sau anumiţi factori obiectivi şi chiar subiectivi. Calculul nuanțat este utilizat în extinderea sistemelor expert pentru a permite raționamentul asupra unor cunoștințe formulate imprecis specificate prin variabile lingvistice sau numere fuzzy.
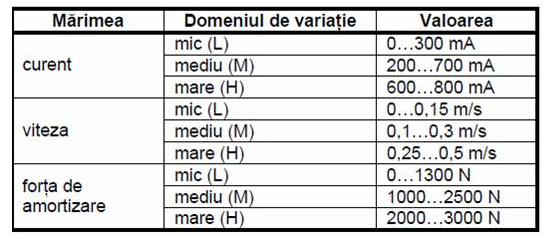
Un exemplu de utilizare a variabilelor lingvistice, în tehnică, este prezentat în tabelul [4]:
Bibliografie
1. Zadeh, L. A. (1965). "Fuzzy sets". Information and Control. 8 (3): 338–353. doi:10.1016/S0019-9958(65)90241-X.
2. Vaduva I., Albeanu G., Introducere în modelarea fuzzy, Editura Universității București, 2004.
5. ***, http://www.scritub.com/tehnica-mecanica/Roboti-Industriali-Sisteme-de-45327.php